Это перевод оригинальной статьи от Jesus Castello.
Временна́я сложность алгоритмов — одна из самых интересных концепций в информатике, для понимания которой вам не нужна учёная степень.
Благодаря этой концепции, вы будете способны понять, почему конкретная программа работает медленно, и как вы можете ускорить её.
Вы сможете применить это знание к своему коду.
Эта концепция лежит в основе всех тех причудливых алгоритмов, которые вы можете найти в книгах по информатике, как я продемонстрирую вам позже в этой статье.
Но для начала, мы должны обсудить, что такое медленно и быстро.
«Медленно» против «быстро»
Сортировка одного миллиона чисел за 150 мс (миллисекунд) это медленно или быстро?
Я думаю, что это достаточно быстро, но это не тот вопрос, на который пытается ответить временна́я сложность.
На самом деле, мы хотим узнать, как быстро будет работать алгоритм по мере роста «размера входных данных».
Когда мы говорим о входных данных, мы говорим об аргументах для функции или метода. Если метод принимает одну строку как аргумент, значит это входные данные и длина строки — это их размер.
Нотация «О» большое
Использую нотацию через «О» большое, мы сможем классифицировать алгоритмы по их производительности.
Это выглядит как-то так:
O(1)
Здесь представлен алгоритм константного типа.
Это означает, что алгоритм будет тратить одно и то же время от начала и до конца, независимо от того, сколько работы он должен сделать.
Другой тип — линейные алгоритмы:
O(n)
Здесь «n» представляет размер входных данных (размер строки, массива и т.д.) Это означает, что он будет тратить время в соотношении 1:1 к размеру входных данных, таким образом, что удвоение количества входных данных, приведёт к удвоению времени работы алгоритма.
Вот типы алгоритмов:
(Большинство, но далеко не все, — прим. пер.)
O(1) — константный
Всегда занимает одно и то же время
O(log n) — логарифмический
Объём работы делится на 2 после каждой итерации цикла (пример: бинарный поиск)
O(n) — линейный
Время на совершение работы растёт в соотношении 1:1 от размера входных данных
O(n log n) — линейно-логарифмический
Это вложенный цикл, где внутренний цикл выполняется за log n раз. Примерами могут служить: быстрая сортировка, сортировка слиянием и пирамидальная сортировка.
O(n²) — квадратичный
Время выполнения растёт в квадратичной зависимости от размера входных данных. Вы можете опознать этот алгоритм по циклу обрабатывающему все элементы массива и имеющему вложенный цикл, который на каждой итерации внешнего, также обрабатывает все элементы массива.
O(n³) — кубический
Похож на квадратичный, но время растёт в кубической зависимости к размеру входных данных. Реализация таких алгоритмов, зачастую имеет целых три вложенных цикла.
O(2ⁿ) — экспоненциальный
Время на выполнение таких алгоритмов растёт в степени n к размеру входных данных. Это гораздо медленнее, чем квадратичный алгоритм, так что не путайте их. Одним из примеров может служить рекурсивный алгоритм Фибоначчи.
Анализ алгоритмов
Вы можете начать развивать свою интуицию в этой области, если вообразите входные данные, как массив из n элементов.
Представьте, что вы хотите найти все элементы, которые будут чётными числами. Единственный способ достичь этого — проверить каждый элемент массива.
1
[1,2,3,4,5,6,7,8,9,10].select(&:even?)
Вы не можете пропускать числа, потому что вы можете упустить те, которые ищете. Так что, это условие делает данный алгоритм линейным — O(n).
Три разных решения одной и той же проблемы
Анализ конкретных примеров может быть довольно интересным, но что действительно помогает понять эту идею, это разбор того, как мы можем разными способами решить одну и ту же проблему.
Мы собираемся исследовать три примера кода для проверки решений в игре Scrabble.
Scrabble — это игра, которая получив список символов (пример: o, l, l, h, e), просит вас сложить слово (пример: hello) используя эти символы.
Вот первое решение:
1
2
3
def scrabble(characters, word)
word.each_char.all? { |c| characters.count(c) >= word.count(c) }
end
Знаете ли вы временную сложность этого кода? Ключ для понимания — метод count, так что убедитесь, что вы понимаете, что этот метод делает.
Правильный ответ: O(n²).
И причина этого в том, что методом each_char мы перебираем каждую букву в строке word. Если бы мы использовали только этот метод, это был бы линейный алгоритм O(n). Но внутри блока мы вызываем метод count.
Этот метод, по сути, является ещё одним циклом, который перебирает символы в строке, чтобы подсчитать их.
Второе решение
Ладно.
Можно ли нам сделать это лучше? Если ли способ избавить нас от этого зацикливания?
Вместо подсчёта символов, мы могли бы удалять их и, таким образом, мы бы проходили через меньшее число символов.
Вот второе решение:
1
2
3
4
def scrabble(characters, word)
characters = characters.dup
word.each_char.all? { |c| characters.sub!(c, "") }
end
Это уже чуть более интересно. Это будет гораздо быстрее чем использование count в случае, когда искомые символы находятся в начале строки.
Но если искомые символы оказываются в конце, в порядке, обратном тому, как они могут находиться в word, производительность может оказаться на уровне первой версии с count, так что мы можем сказать, что это всё ещё квадратичный алгоритм — O(n²).
Нам не нужно беспокоиться о случае, когда нет ни одного из искомых символов в word, потому что метод all? остановится, как только sub! вернёт false. Но вы можете узнать об этом только если будете изучать Руби глубже, чем это дают на обычных курсах.
Давайте попробуем другой подход
Что если мы исключим любые виды циклов внутри блока? Мы могли бы использовать хэши вместо них.
1
2
3
4
5
6
def scramble(characters, word)
available = Hash.new(1)
characters.each_char { |c| available[c] += 1 }
word.each_char.all? { |c| available[c] -= 1; available[c] > 0 }
end
Чтение и запись значений хэша это всегда константная операция — O(1), что достаточно быстро, особенно в сравнении с циклами.
Мы всё ещё имеем два цикла:
Один строит хэш, второй проверяет её. Но так как эти два цикла не вложены друг в друга, это линейный алгоритм — O(n).
Если мы проведём бенчмарк этих трёх решений, мы увидим, что наш анализ соответствует результатам:
1
2
3
hash 1.216667 0.000000 1.216667 ( 1.216007)
sub 6.240000 1.023333 7.263333 ( 7.268173)
count 222.866644 0.073333 222.939977 (223.440862)
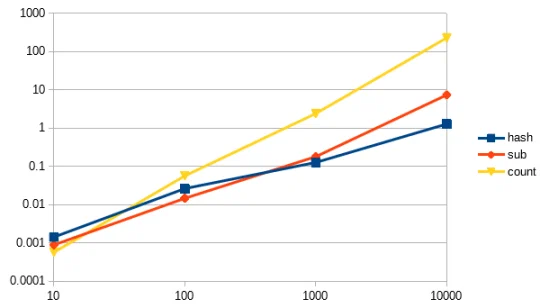
Вот линейный график:
Обратите внимание на следующее:
- Ось Y (вертикальная) показывает, сколько секунд заняло выполнение алгоритма, в то время как ось X (горизонтальная) показывает размер входных данных.
- График приведён в логарифмическом масштабе, который сжимает значения в определённом диапазоне, так что на самом деле, линия count загибается вверх намного резче.
- Причина, по которой я использовал логарифмический масштаб, заключается в том, что я хотел показать интересный эффект, когда способ с методом count оказывается быстрее всех, если мы имеем очень маленький размер входных данных.
Выводы
Вы узнали о временно́й сложности алгоритмов, нотации с большим «О» и анализе временно́й сложности. Также вы увидели несколько примеров, в которых мы сравнили различные способы решения одной и той же проблемы и проанализировали их производительность.
Надеюсь, вы узнали что-то новое и интересное для вас!
Спасибо, что прочитали до конца.
Источник: The Definitive Guide To Time Complexity For Ruby Developers